--- TUGAS BLOG ALGO-BINUS Mingguan ---
BINARY SEARCH TREE
-------------------------------------
Dalam binary search tree, intinya adalah data-data tersebut terurut. Biasanya uruta-urutan data/node/elemen tersebut adalah:
- Subtree kiri mengandung semua elemen yang lebih kecil dibanding subtree kanan
- Subtree kanan mengandung semua elemen yang lebih besar dibanding subtree kiri
Karena intinya terurut, maka bisa juga sebaliknya, namun, yang lazim dan biasa digunakan saat ini adalah subtree kiri selalu mengandung elemen yang lebih kecil dibanding subtree kanan.
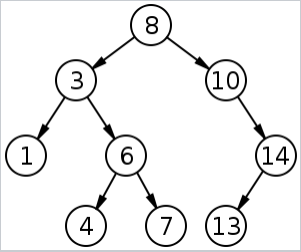
contoh BST:
-------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------
1. Binary Search Tree (BST)
Binary Search Tree (BST) merupakan salah satu struktur data yang mensupport metode pencarian(searching) dan pengurutan(sorting) secara cepat, serta penambahan atau pengurangan data/elemen secara mudah. BST juga diketahui sebagai binary tree yang terurut.
2. Sifat Binary Search Tree
Dalam binary search tree, intinya adalah data-data tersebut terurut. Biasanya uruta-urutan data/node/elemen tersebut adalah:- Subtree kiri mengandung semua elemen yang lebih kecil dibanding subtree kanan
- Subtree kanan mengandung semua elemen yang lebih besar dibanding subtree kiri
Karena intinya terurut, maka bisa juga sebaliknya, namun, yang lazim dan biasa digunakan saat ini adalah subtree kiri selalu mengandung elemen yang lebih kecil dibanding subtree kanan.
contoh BST:
3. Operasi Binary Search Tree
Berikut merupakan operasi-operasi dasar dalam binary search tree:
- find(x) : untuk menemukan key x dalam BST
- insert(x) : untuk memasukkan/insert key x yang baru ke dalam BST
- remove(x) : untuk menghapus/menghilangkan key x dalam BST
4. Operasi Search/Find
Karena sifat dari BST, pencarian / searching / finding yang dilakukan dalam tree mmenggunakan BST menjadi mudah. Berikut algoritma pseucode ketika kita hendak mencari dimana X:
- Memulai dari root
- Jika root merupakan X, maka proses selesai
- Jika X lebih kecil dari root, maka pencarian dilanjukan ke subtree kiri, tapi jika X lebih besar dari root, maka dilanjutkan pencarian ke subtree kanan, begitu seterusnya hingga ditemukan X.
5. Operasi Insertion
Memasukkan/inserting data/node/elemen kedalam BST diselesaikan sebacar berulang. Berikut algoritma pseucode memsukkan key X ke dalam BST:
- Dimulai dari root
- Jika X lebih kecil dari root atau node, X di masukkan ke bagian kiri subtree, jika X lebih besar maka ditempatkan ke bagian kanan subtree, hal ini terus dilakukan hingga ditemukan ruang kosong dalam tree untuk memasukkan X (X menjadi leaf baru).
Contoh: memasukkan key(35)
6. Operasi Delete
Dalam penghapusan node/elemen/data (contohnya: penghapusan key X) dalam BST, ada 3 pertimbangan:
1. Jika key X merupakan leaf(data paling bawah dalam tree), maka kita hapus data/leaf tersebut.
2. Jika key X merupakan node dengan satu anak, maka hapus node tersebut dan kemudian hubungkan anak dari X dengan parent dari X.
3. Jika key X merupakan node dengan dua anak, maka cari data paling kanan bawah(value paling tinggi) dari subtree sebelah kiri, kemudian replace/tukar dengan data tersebut dengan key X, lalu hapus key X, atau bisa menggunakan data paling kiri bawah (value paling kecil) dari subtree sebelahh kanan lalu replace/tukar data tersebut dengan key X lalu hapus key X.
contoh: deleting key(21)
contoh 2: delete key (37)
contoh 3: delete key(30)
-------------------------------------------------------------------------------------------------------------
Referensi:
- Power Point Binary Search Tree
- https://en.wikipedia.org/wiki/Binary_search_tree
-------------------------------------------------------------------------------------------------------------
Berikut adalah tugas mingguan membuat blog berisi rangkuman materi Binary Search Tree yang telah saya pelajari.
Sekian,
Sekian,
---Terima kasih.---
Nama: Felina Suryadi
NIM: 2301914604
Kelas Besar: CB01
-------------------------------------------------------------------------------------------------------------










Tidak ada komentar:
Posting Komentar